文字列中の繰り返し構造

繰り返し構造

　文字列w=aababaaの中のababaはabの2.5回の繰り返しです。繰り返しにはちょうど２回の繰り返しであるスクエアや、ちょうど３回の繰り返しであるキューブなどがあります。繰り返しの最初の１回分をその繰り返しの根と言い、根の長さを周期と言います。文字列が他の文字列の整数回の繰り返しではないとき、その文字列は素であると言います。次の図の文字列aaaabbabaが含むスクエアはaa, aaaa, bb, babaであり、それぞれの周期は1,2,1,2です。スクエアbabaの根baは素ですが、スクエアaaaaの根はaaでaの2回繰り返しなので素ではありません。また、この文字列はキューブaaaを含んでいます。

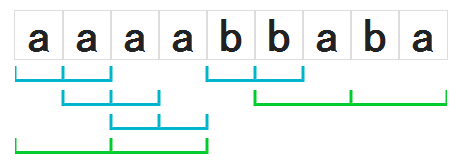
文字列aaaabbabaが含むスクエア

　根が素であり、同じ周期では左右に延長できない繰り返しを連と言います。連の繰り返し回数を連の指数と言います。文字列ababaaaaについて、ababa, aaaaはそれぞれ周期2, 1、指数2.5, 4の連です。繰り返しababは右に1文字延長したababaが同じ周期2の繰り返しであるため、連ではありません。根が素であるという条件から、aaaaは周期2で指数2の連ではなく、周期1で指数4の連と考えます。拙作のプログラムで文字列中の連やスクエア、回分を可視化して見ることができます。

文字列ababaaaaが含む連

　ある長さnの文字列が最大何個の連を含むのか？というのは未だ未解決の問題です。我々が発見した長さ125文字の文字列は、次のように110個の連を含みますが、111個の連を含む長さ125文字の文字列が存在するか否かは分かっていません。ある長さnの文字列はn個以上の連を含まないと予想されていますが、証明はなされていません。

110個の連を含む125文字の文字列（クリックで拡大）

連の指数和の平均値／スクエアの平均個数

　長さがnで、アルファベットサイズ（文字の種類数）がσの文字列が含む連の平均個数を考えます。例えばn=4, σ=2について、文字列は2⁴=16個あり、それぞれ次のように連を含んでいます。よって連の平均個数は(1+1+1+2+1+1+1+1+1+1+1+1+2+1+1+1)/16=1.125個です。

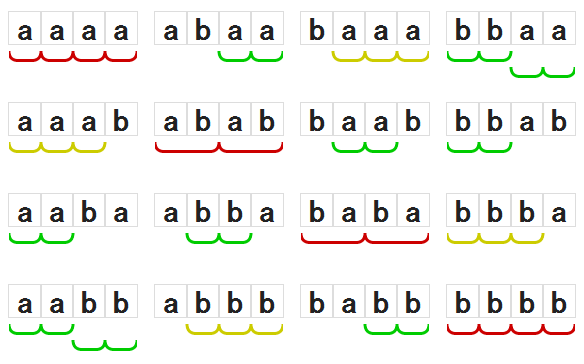
長さ4アルファベットサイズ2の文字列と連

　連の最大個数の厳密な値は知られていませんが、長さnアルファベットサイズσの文字列が含む連の平均個数Rs(n,σ)は

$R_s\left(n,\sigma\right) = \sum_{p=1}^{\frac{n}{2}} \sigma^{-2p-1} \left((n-2p+1)\sigma-(n-2p)\right) \sum_{d|p} \mu\left(\frac{p}{d}\right) \sigma^d$

と表せることが示されています^[1]。ここで、μ(n)はメビウス関数です。

　我々は連の指数の和の平均を考えました。例えば、長さが4アルファベットサイズが2の文字列の連の指数和の平均は上の図から、 (4+3+2+4+2+2+2+3+3+2+2+2+4+2+3+4)/16=2.75です。長さがn、アルファベットサイズがσの文字列が含む連の指数和の平均Es(n,σ)が、

$E_s(n,\sigma) = \sum_{p=1}^{\frac{n}{2}} \sigma^{-2p-1} \left( 2(n-2p+1)\sigma - \left(2-\frac{1}{p}\right) (n-2p) \right) \sum_{d|p} \mu\left(\frac{p}{d}\right) \sigma^d$

と表せることを示しました^[2]。

　また、連の平均個数と連の平均指数和から、根が素なスクエアの平均個数

$S_s(n,\sigma) = \sum_{p=1}^{\frac{n}{2}} \sigma^{-2p} (n-2p+1) \sum_{d|p} \mu\left(\frac{p}{d}\right) \sigma^d$

を導出しました^[3]。

ネックレスが含む連とスクエアの平均個数

　通常の紐状の文字列の両端を繋ぎ、輪にした文字列をネックレスと言います。回転によって重なるネックレスは同じネックレスと見なします。ネックレスは語の組合わせ論的に興味深い種々の性質を持っています。例えば、アルファベットサイズが3の（3種類の文字を使った）文字列を考えたとき、通常の文字列はどのような長さnでもスクエアを含まない文字列が存在しますが、ネックレスではn=5,7,9,10,14,17ではスクエアを含まない文字列が存在せず、その他のnではスクエアを含まない文字列が存在することが知られています^[4]。

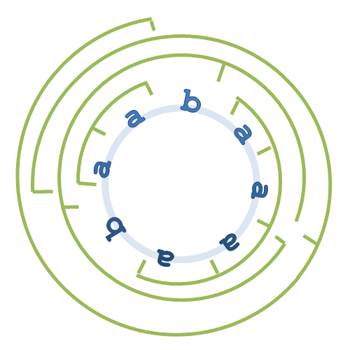
長さ4アルファベットサイズ2の文字列と連
ネックレス<abaaaaba>が含む連、aa, aaaa, aabaabaa, aabaaaabaa

　我々はこのネックレスが含む繰り返し構造について研究を行い、スクエアの平均個数と連の平均個数、連の指数和の平均値を導出しました^[5]。例えば、長さnアルファベットサイズσのネックレスが含む連の平均個数は

$R_c\left(n,\sigma\right) = \frac{n}{\sigma^n} \sum_{p=1}^n \sum_{d|p} \mu\left(\frac{p}{d}\right) \delta_r\left(n,p,d,\sigma\right)$

として、

$R_c\left(n,\sigma\right) = \frac{n}{\sigma^n} \sum_{p=1}^n \sum_{d|p} \mu\left(\frac{p}{d}\right) \delta_r\left(n,p,d,\sigma\right)$

と表すことができます。ここで、φ(n)はオイラーのトーティエント関数、

$\delta_r\left(n,p,d,\sigma\right) = \begin{cases}(\sigma-1)\sigma^{d-2p+n-1} & \text{if $d > 2p-n$ and $d \not\equiv 0 \pmod{d-(2p-n)}$,} \\ 0 & \text{otherwise.} \end{cases}$

です。

参考文献

Simon J. Puglisi and Jamie Simpson.
The expected number of runs in a word,
Australasian Journal of Combinatorics, 42, pp. 45-54, 2008.
Kazuhiko Kusano, Wataru Matsubara, Akira Ishino, and Ayumi Shinohara.
Average Value of Sum of Exponents of Runs in Strings,
Proceedings of the Prague Stringology Conference 2008 (PSC 2008), pp. 185-192, September 2008.
Kazuhiko Kusano, Wataru Matsubara, Akira Ishino and Ayumi Shinohara.
AVERAGE VALUE OF SUM OF EXPONENTS OF RUNS IN A STRING,
International Journal of Foundations of Computer Science (special issue for Prague Stringology Conference), Vol. 20, Issue 6, pp. 1135-1146, December 2009.
James D. Currie.
There are ternary circular square-free words of length n for n≧18,
THE ELECTRONIC JOURNAL OF COMBINATORICS, 9, #N10, 2002.
Kazuhiko Kusano and Ayumi Shinohara
Average Number of Runs and Squares in Necklace,
Proceedings of the Prague Stringology Conference 2010 (PSC 2010), pp. 167-177, September 2010.

草野　一彦